In a shell and tube heat exchanger, the tubes play a crucial role in the efficient transfer of heat. Over time, they can experience fouling, which results in a decline in the heat exchanger’s performance. However, within the realm of heat exchangers, a process known as retubing can be performed. Retubing is a standard maintenance procedure widely practiced in the industry, aimed at prolonging the lifespan and enhancing the efficiency of these heat exchanger components.
By Ángel Meroño García – Technical Officer, Mecanicas Bolea
Before retubing, a comprehensive thermal analysis is essential. Optimal outcomes are typically achieved when using identical tubes: same material, same external diameter, and same thickness. Altering these parameters can lead to unexpected shifts in thermal performance. These shifts can either improve or diminish efficiency.

In this article, we take a practical approach by presenting a real-world case study. This case study offers a concrete example of the intricacies involved in the retubing process within industrial applications. Join us as we delve into the practical aspects of heat exchanger rejuvenation and unveil the captivating world of thermal optimization.
The case
A few weeks ago, I was tasked with evaluating a heat exchanger retubing process thermally. If the same tubes were used for the new bundle, calculations would be unnecessary. However, this was not the case. The new tube specifications called for a material with lower thermal conductivity and a reduction in tube thickness. While such cases are typically resolved by adjusting the input parameters in a specialized software to align with the new requirements, the present scenario triggered this article. The constraints of our model will be established based on this case.
Objective
The aim is to establish a systematic procedure for manually validating the thermal efficiency of retubing, eliminating the need to input all the parameters relating to geometry and fluid properties into the software. This approach may help with a better understanding of how heat is transferred in a heat exchanger. In this context, we have some quantities that inform us about the thermal efficiency of an item. Concerning this article, the so-called overdesign [¹] (or oversize) will be used to estimate the impact of retubing in the exchanger.
The values in Equation 1, as reported in some manuals [²], span from 20% to 40%. However, experience suggests that these values are closer to 10%. This percentage represents a safety margin to ensure that the system can handle unexpected, for instance, peak loads or variations in operating conditions without compromising performance. However, in this study no numerical values will be inputted until the very end. The aim is to give the reader an instinctive perspective when approaching this kind of case. To achieve this, we will conduct symbolic calculations.
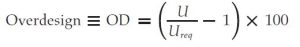
First-stage parameters
One of the challenges when manually calculating heat exchanger parameters is to obtain U accurately. Its value tells us about the ease with which the heat flows from the hot to the cold fluid in a heat exchanger. Typically, bibliography introduces U through the most familiar equation to the designer of heat transfer equipment, derived from Newton’s law of cooling:
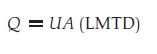
However, for this analysis, it will be presented in a more intuitive way for the reader. In particular, an analogy exists between thermal and electric flow. Just as an electrical resistance is associated with the conduction of electricity, a thermal resistance, 1/U, may be associated with the resistance to heat flux. A difference in voltage can be compared to a difference in temperature. Therefore, 1/U can be expressed as the sum of the individual resistances in a tube [³]:
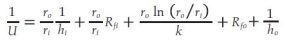
The third term on the right side of the equation corresponds to the resistance due to the tube wall, and it is denoted as:
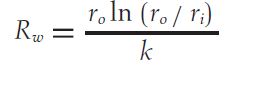
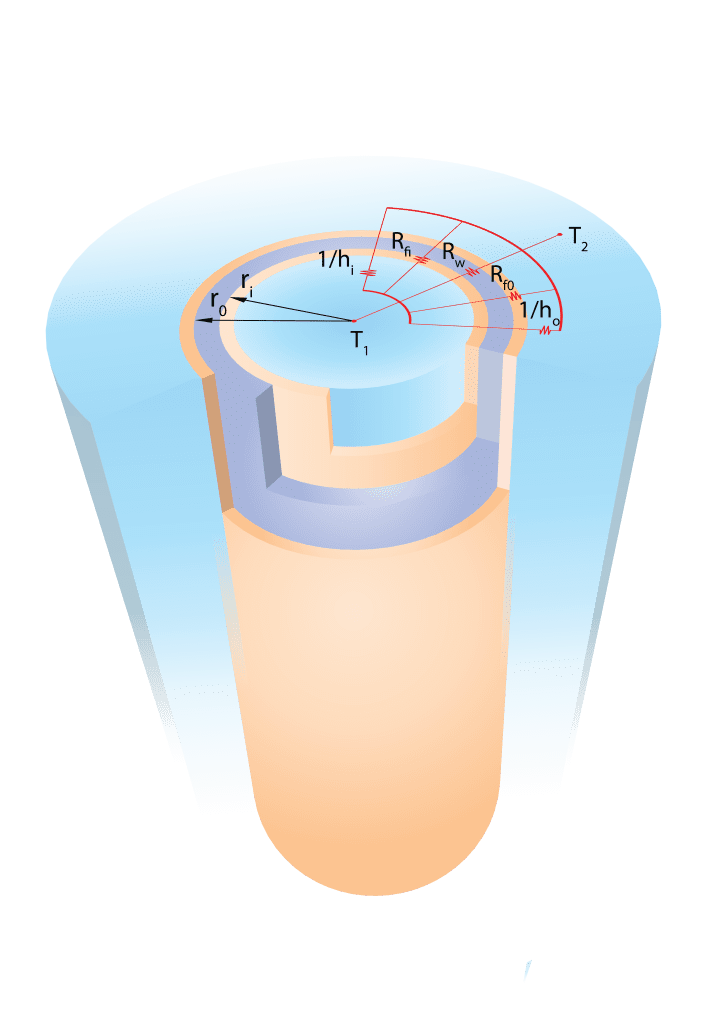
Individual thermal resistances are added in parallel because the heat transfer ratio, Q, is constant through the network. Equation 3 applies for unfinned tubes, where U is based on the outer surface of the tube. The comprehension of this electrical analogy is simplified when observing Figure 1.
In the tube section, we see how each layer is associated with a resistance in our thermal circuit: tube-side fluid, inside fouling, tube wall, outside fouling and shell-side fluid. These resistances act as an obstacle for heat and shape the temperature profile in the system.
Retubing implications
In order to make a first guess for the change in efficiency of the exchanger, some effects must be taken into account. The first consequence we can think of is a change in the tube wall resistance. Equation 4 indicates that the greater the conductivity of the material of the tube, k, the lower Rω will be. Consequently, heat transfer will be enhanced. However, this equation also provides information about the consequences of varying tube thickness. Since the ratio rₒ/rᵢ increases when thickness does, Rω increases as well.
Therefore, two parameters affect to the tube wall resistance: thickness and conductivity. If the retubing process implies maintaining one of the parameters constant, or it increases one and decreases the other, it is relatively straightforward to make the forementioned first guess. There would be only one variable in Equation 4. However, what if both thickness and conductivity decrease? Indeed, this is the real case, and as such, this final scenario will be considered.
If that were not enough, it would be a mistake to overlook tube-side fluid velocity. It decreases with larger inside radius and it plays a significant role in heat transfer processes. Qualitatively, one can observe that as the tube-side fluid velocity experiences an increase, there is a corresponding rise in the heat transfer ratio, Q. Two reasons are that higher velocities allow more turbulence and lower fouling [¹] [⁴].
Gathering the information from this section tells us that the variables determining heat transfer are correlated. In the next sections, a model describing the system will be formulated with the purpose of obtaining practical results.
Heat flux through tube walls
Once the context has been established, we can begin our analysis of the heat transfer mechanism. Equation 4 can be used to obtain a comparison of the tube wall resistances between the old and new tubes. We will employ a prime notation to denote values associated with the new tubes. For instance, wall resistance in the new tubes is represented as Rω’.
To relate this article with the real case, it will be assumed that rₒ = rₒ’ and k’ < k. This means same tube outer radius and a lower conductivity for the new tubes. After some mathematical manipulation, the thickness, t’, for which Rω’ = Rω can be found:
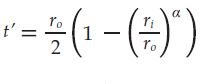
In the equation, α = k’/k. Equation 5 concludes that exceeding this value for thickness, given both conductivities, leads to more difficulty for heat to flow through the tube wall after the retubing procedure. However, as it was mentioned, this does not explain heat transfer completely. Understanding the system as a whole requires the thermal analysis of the tube-side fluid.
Convection in tube-side fluid
In the preceding section, while not explicitly stated, we were talking about conduction heat transfer, which is the primary mechanism employed by solids for internal heat transfer. If a fluid is what is being studied, then convection takes place.
Among all the properties that conform to the thermophysical identity of the fluid circulating through the tubes, we will center our attention on a variable that may have gone unnoticed when we introduced Equation 3. This is the tube-side fluid convection coefficient, hi. It is an indicator of how effective convection is. Obtaining this parameter, as well as ho, results in a delicate task to accomplish. The reason is that fluid dynamics and, consequently, turbulent flow, come into play. In an attempt to show the complexities that turbulence introduces into calculations, we will reference the 20th-century famous scientist, Werner Heisenberg, who stated [5]:
“When I meet God, I am going to ask him two questions: Why relativity? And why turbulence? I really believe he will have an answer for the first.”
The difficulty in precisely calculating hi, led researchers to consider empirical methods to obtain this coefficient. It is our task to make use of the existent equations to apply them to our case.
An empirical approach
When aiming to calculate hᵢ, specialized bibliography on heat exchanger design provides us with the ingredients to be mixed to find it. This means to choose the equation that better describes the flow regime of the fluid. The criteria to select the proper equations must be carefully considered if we want to represent reality. For our case, a single-phase fluid, with constant physical properties will be considered in a fully turbulent flow in straight tubes.
The way to proceed in this type of problem is to calculate the Nusselt Number, a useful dimensionless parameter in fluid mechanics, to solve the equation that defines Nu for hᵢ.

Now we need an empirical equation that represents our case and gives us Nu. Opting for the Dittus–Boelter equation [³] proves to be a sound selection in this regard.
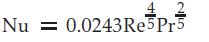
Equation 7 introduces two more dimensionless parameters: the Reynolds Number and the Prandtl Number. However, a deeper analysis of these numbers is beyond the scope of this article. After combining Equations 6 and 7, the following relation is found for hᵢ’:
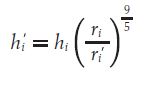
I encourage the reader to obtain the equation defining these parameters and follow the outlined steps to derive Equation 8. It tells us that a decrease in the tube wall thickness leads to a less efficient heat transfer from the fluid in the tubes. This is explained because, for the same flow rate, an increase in the inside radius provides a bigger area and a reduction in velocity. As mentioned previously, low velocities are not effective in transferring heat.
Impact on heat transfer

Up to this point, our focus has been on examining the changes in specific thermal resistances after retubing. However, a more insightful approach is to calculate the variations in the overall heat transfer coefficient, as this will elucidate how overdesign may be altered.
If we depart from Equation 1, it can be mathematically proven that the ratio in overdesign is equivalent to the ratio in the coefficient U after the retubing:
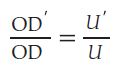
It is now easier to examine how well or poorly heat will be transmitted with the new tubes. An interesting approach is to study Equation 10 by inputting numerical values, in order to obtain a visual insight into the fluctuation in overdesign. All these values in the equation are known from the existing tubes and only hi’ should be substituted using Equation 8. It’s important to highlight that in this specific scenario, the convection coefficient for the shell-side fluid remains constant. This property arises because the fluid’s composition remains unchanged, and the geometry it interacts with does not change [⁶].
Effects on overdesign
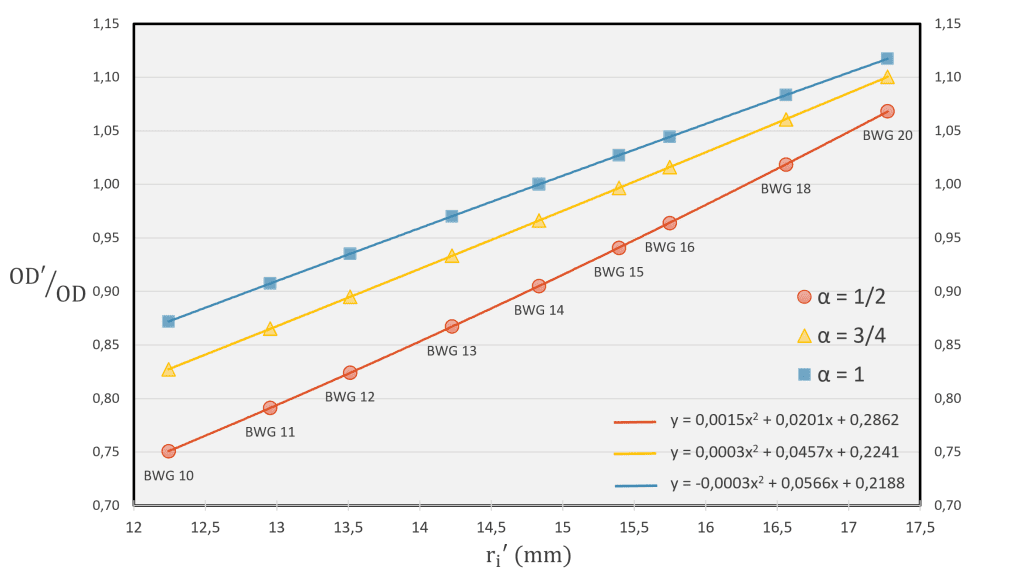
At this point, we are ready to delve into the impact of retubing in overdesign. We will consider three different values for α: 1/2, 3/4 and 1. Regarding the tube geometry, the outer radius will be ¾”. To model the real scenario, the values for the inner radius are consequently set with the Birmingham Wire Gauge (BWG) system [⁶]. Regarding the real case, BWG 14 is the value prior to retubing. In Figure 2 it can be clearly appreciated that, in the range of interest, the ratio in overdesign increases with ri’. With this representation, it can be easily appreciated how higher conductivities provide better heat transfer.
To read this graph, it is helpful to see that α = 1 and BWG 14 represents the previous case, so the OD ratio is equal to one. It is worth noting that the curves align exactly with a quadratic polynomial, hinting at the potential for future research to extract precise overdesign values from this behaviour.
Smart decision-making
We have observed how subtle alterations in tube specifications can set in motion a series of effects on heat transfer efficiency. These alterations usually arise from business or economic decisions, and in those contexts they are perfectly valid. However, from an engineering perspective it may not be the case.
This study intended to give the reader information beyond the economic regarding a retubing process. This was achieved by carefully analysing individual thermal resistance behaviour and their effect on the total heat transfer. To ensure the study’s accuracy, a retubing simulation was made with a specialized software. The results obtained were highly satisfying.
The proposed method is an option which may be considered along with other perspectives to enhance decision-making in the industry. It can be particularized for any situation and become a worthwhile tool for such cases.
About the author
 Ángel Meroño García is a physicist at Mecánicas Bolea. He specializes in thermal calculations, optimizing systems to industry standards. Collaborating with a skilled team, Ángel focuses on delivering tailored solutions for clients. Feel free to reach out to Ángel for any clarifications relating to this article.
Ángel Meroño García is a physicist at Mecánicas Bolea. He specializes in thermal calculations, optimizing systems to industry standards. Collaborating with a skilled team, Ángel focuses on delivering tailored solutions for clients. Feel free to reach out to Ángel for any clarifications relating to this article.
References
- Bennett, Christopher & R.S, Kistler & Lestina, & King, D.(2007). Improving heat exchanger designs. Chemical Engineering Process. 103. 40-45.
- Kuppan T. Heat Exchanger Design Handbook. New York: Marcel Dekker; 2000.
- Frank P. Incropera, Dewitt, Bergmann, Lavine. Fundamentals of heat and mass transfer, 6th ed, 2010.
- Jradi, Rania & Marvillet, Christophe & Jeday, Mohamed-Razak. (2022). Fouling in Industrial Heat Exchangers: Formation, Detection and Mitigation. 10.5772/intechopen.102487.
- Cassidy, D. Uncertainty: The Life and Science of Werner Heisenberg. New York: W. H. Freeman, 1991.
- Standards of the Tubular Exchanger Manufacturers Association, Tenth Edition, 2019, TEMA, Inc.

