Use of FEM analysis for safety-critical applications

Among air-to-fluid heat exchangers, the finned block type with tubular headers is commonly recognized as the most versatile, as it gives maximum freedom in configuring the circuiting, in order to achieve the best thermodynamic performance.
On the other hand, it bears some intrinsic structural weaknesses, namely in the connection between the tubular headers and the exchange tubes, achieved by means of short sections of tube that we will call ‘stubs’. Typically, both the stubs and the exchange tubes are smaller and thinner than the headers. Moreover, their weakness is somewhat amplified when copper, which has a relatively low-tensile strength, is used as material – a common choice, as copper is the best performer when speaking of heat exchange.
Indeed, a tubular header can be considered as a mass subject to its own weight (its content included) that is held in place by the stubs. It is evident how the header, when stressed by external loads, transmits them to the stub tubes and, in turn, to the exchange tubes. Therefore, it is important to limit the loads that the piping exerts on the headers, eventually using reinforcements or flexible joints; something that is not particularly difficult to achieve within standard civil HVAC installations.
The scenario is much different when it comes to high-demand applications where resistance – functional resistance, in many cases – is required to withstand exceptional events such as earthquakes, explosions, shocks, tornadoes and their aftermaths. These are typical requirements for heat exchangers intended to be used in nuclear power plants, military ships, and oil & gas offshore installations, where also HVAC is considered a safety-critical equipment (as an example, think about keeping liveable conditions in nec-essarily segregated control rooms during nuclear accidents or CBNR attacks).
On the other hand, another typical requirement for such applications is lightness. Therefore, a thorough reinforcement of the heat exchanger by means of an indiscriminate addition of material (thicknesses, reinforcements, etc.) as a design by a formulae approach would suggest, is not the solution.
Alternative design approaches are needed, with the aim to design thin-walled equipment, reinforced only when required, where required, and to the required extent; in other words, any bit of material used in manufacturing shall be there because it is needed, avoiding over-engineering as much as possible.
As a consequence, such an approach at the design stage necessarily entrains considering states of stress of the material that are close to its critical one. Therefore, the calculation for stability and stiffness of the component becomes so crucial that numerical analysis methods have become the solution. Indeed, the heat exchanger is subject to a number of loads (pressure, differential thermal dilatation, external loads, plus the loads due to exceptional events) that have to be combined in order to assess its suitability. As such, FEA, Finite Element Analysis, is the preferred approach, supplemented by CFD, Computational Fluid Dynamics analysis, where needed.
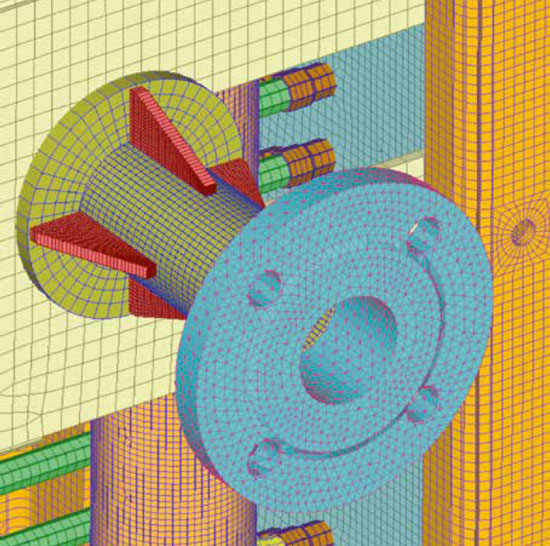
Here, in order to provide a brief presentation of the use of FEA in designing heat exchangers, we study a sample case where seismic functional resistance (i.e.: the heat exchanger is also capable of performing its service during an earthquake) is required and see how the simulation ran. The aim of the simulation is to reproduce seismic activity in a realistic way, so as to demonstrate whether the heat exchanger can resist the stresses coming from such event. To this purpose, the exchanger must be accurately modelled and properly meshed; a precise and regular meshing is crucial in order to avoid numerical errors arising from poor meshing. Fig. 1 shows an abstract from the meshed model of a heat exchanger, in the area of its connection and of the nearby stub tubes.

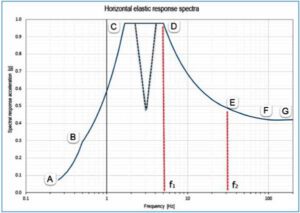
The analysis requires the calculation of the eigenvalues to consequently determine the natural modes of vibration (see Fig 2), and assess whether (or where) the heat exchanger lies in the flexible range or in the rigid one. Such information is deduced from the seismic spectrum (see as example in Fig. 3), where the damping of the material is around 2–5%. Analysing Fig. 3, the periodic (flexible) response corresponds to ranges AB, BC and CD (low frequencies, until f1), while the rigid one shows up in ranges EF and FG (high frequencies, from f2 on). There is a mixed-response (periodic and rigid, range DE) between f1 and f2. In terms of vibration theory, the rigid response corresponds to the steady phase of dynamic stress response. Dashed blue lines refer to a possible case of seismic response spectrum having two (or more) acceleration peaks (so called multiple-peak spectrum)
In the specified case, the natural frequency of the first vibration mode is lower than f2, and therefore a dynamic calculation is required, as the heat exchanger will actively participate to the seismic event.
Here, we consider the simpler case where the frequencies are higher than f2; in lieu of the dynamic calculation, a pseudo-static analysis (such as Static Coefficient Method SCM, Equivalent Static Methods ESM et al.) can be performed, multiplying the loads by 1.5 and performing it in each of the three directions X, Y and Z.
The modal responses of a seismic event are then combined in the three directions according to one of the following rules:
SRSS, acronym for “Square Root of Sum of Squares”; CQC, acronym for “Complete Quadratic Combination”. Generally, SRSS is the preferred mode when the modal frequencies are well separated. It becomes less dependable when the frequencies come closer. In the latter case the SRSS is chosen.
The combined seismic effect obtained as above, is then further combined linearly with the other possible bound-ary conditions set by the project specifications (design pressure, external loads, etc.)

A comparison between the calculated stresses and the allowable ones, which assess the suitability of the heat exchanger, are performed according to a method that is specified by the reference standards applicable to a specific project. However, in general, the method of choice is one of the two specified here below:
a) The Von Mises yield criterion method (also known as the maximum distortion energy theory).

In terms of the principal stresses (σ_nn), the Von Mises criterion is expressed as:

where S_VM is the Von Mises stress or equivalent tensile stress.

The Von Mises criterion is particularly suited to the analysis of ductile materials like metals in general.

b) The Tresca yield criterion (also known as the maximum shear stress theory).

In terms of the principal stresses (σ_nn), the Tresca criterion is expressed as

where S_T is the Tresca stress.

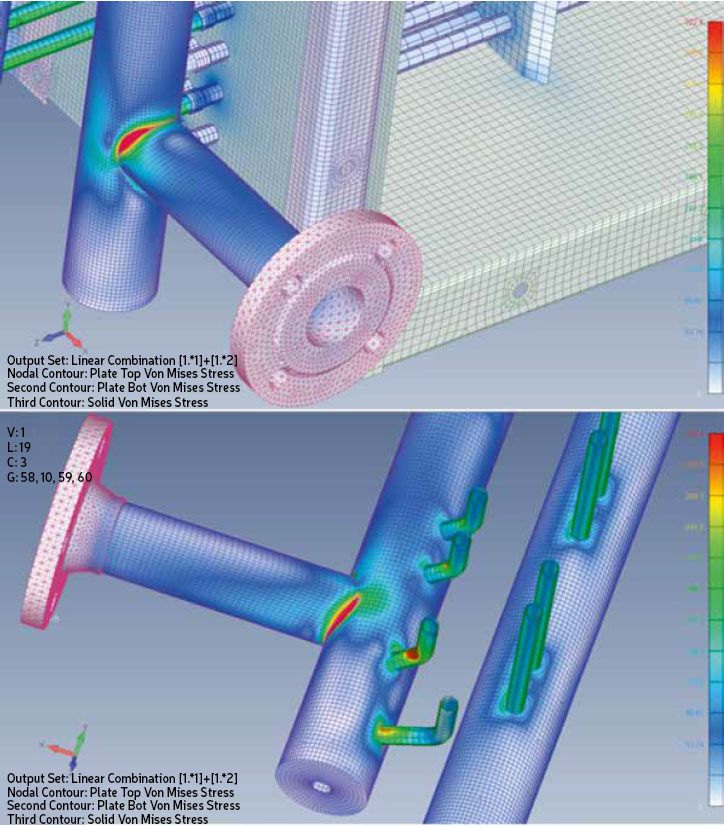
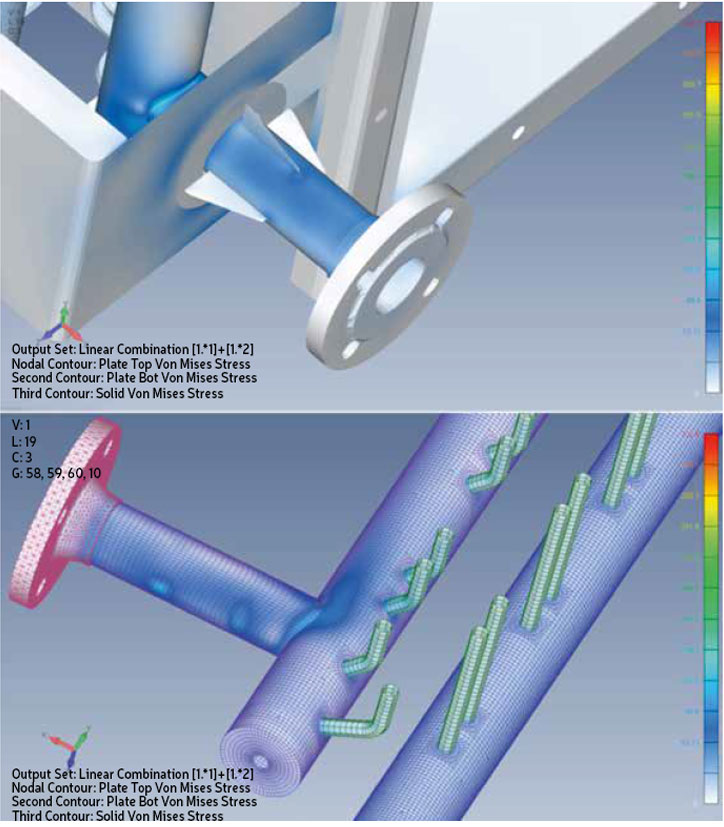
Figs. 4 and 5 show a comparison of the stresses applied on the same heat exchanger, using the same loads (the stress/color scale is the same) respectively without reinforcements and with the reinforcements designed according to the outcome of a FEA assessment.

Fig. 6 summarizes in tabular form the outcome of the analysis, summarizing the maximum stresses and comparing them to the ones allowable at design conditions for each material.

It is evident that without reinforcement the stub tubes and the connection joint would have to bear a too high level of stress that would not be acceptable. Therefore, a localized and properly engineered reinforcement structure, though relatively thin-walled, can be used to avoid the need for the adoption of thicker-walled components (tubes, headers).

In conclusion, Finite Element Analysis provides the way to deliver the most efficient custom-designed finned block heat exchangers for those applications where both lightness and safety are required, without coming to compromises.